Permute 3.0 – fast file conversion in a slick interface!
As a professor teaching media arts and animation courses, I do a lot of file conversion. This is especially true when processing files in batch: whether it’s taking AVI’s from Maya and converting them to .mp4 format, or converting a truckload of PSDs into JPGs. In the past, I would write my own Photoshop action to batch convert images. Later, I used Bridge. But I wanted a conversion tool that will let me process both still images and movie files, in a quick and convenient way.
Enter Permute by Charlie Monroe Software. This $35US app (currently at version 3.5.15) is a conversion powerhouse. I’ve used it for the better part of a month now and find its features to be indispensable for the type of work I do.
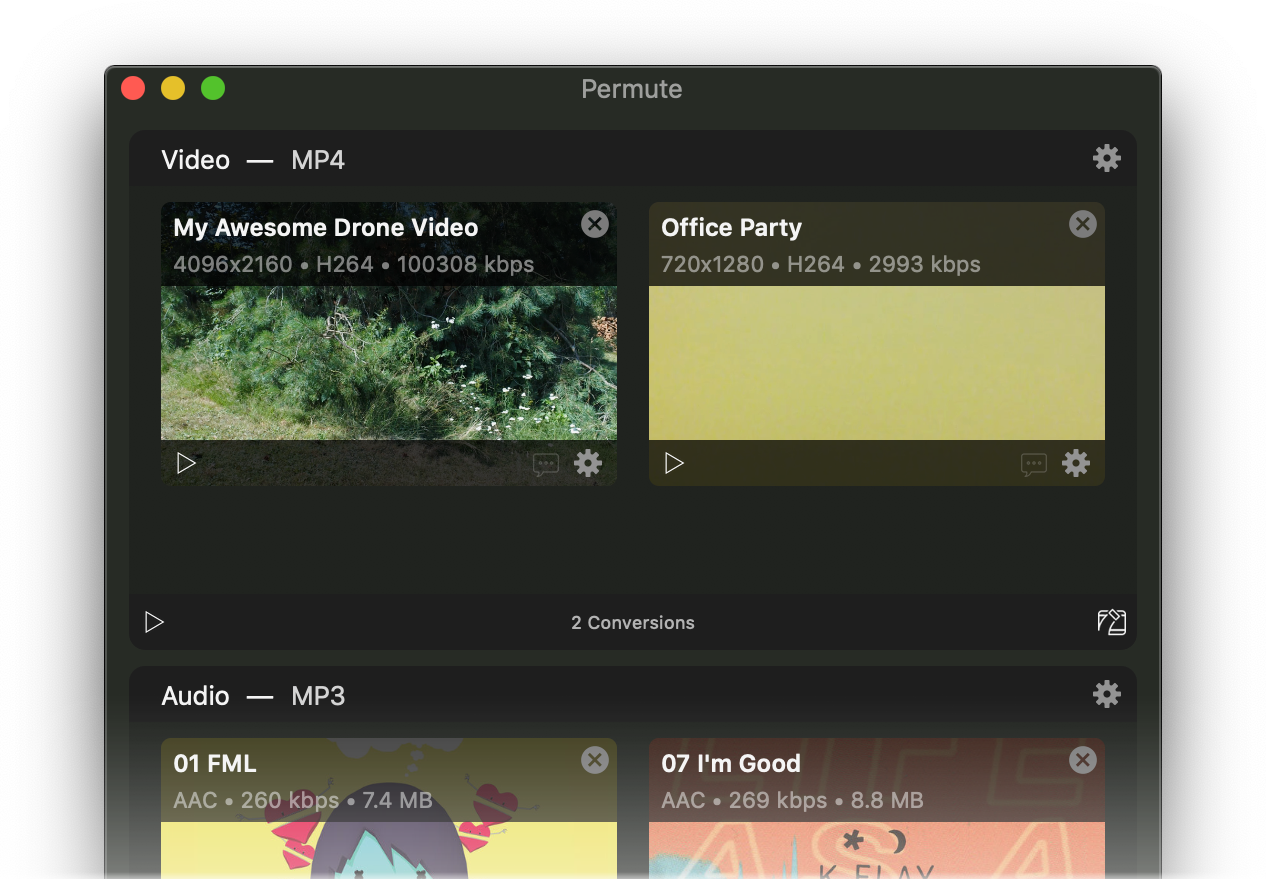
Permute is simple to use. First, grab images and movies that you want to convert and drag them into Permute’s main window (the one with the cute robot head).
Next, click on the small gear on the top right to select your conversion options. Hit “Play” and your newly converted files will appear right next to their originals. Conversion is wicked fast – making it ideal of batch processing.
Following this algorithm, the next lexicographic permutation will be 1,3,2,4, and the 24th permutation will be 4,3,2,1 at which point ak permutation. This method uses about 3 comparisons and 1.5 swaps per permutation, amortized over the whole sequence, not counting the initial sort. The number of permutations of n distinct objects, taken r at a time is: n P r = n! = (7) (6) (5) = 210 Thus, 210 different 3-digit numbers can be formed from the digits 1, 2, 3, 4, 5, 6, and 7. The top 3 will receive points for their team. How many different permutations are there for the top 3 from the 12 contestants? For this problem we are looking for an ordered subset 3 contestants (r) from the 12 contestants (n). We must calculate P(12,3) in order to find the total number of possible outcomes for the top 3. 3.1 Feb 13, 2019. New: Permute's Workshop - a new powerful feature that adds various new features to Permute. New: Initial workshop modules include PDF filter application, IP camera H.264 fix-up, MP4 web optimization and video/audio track export. Many other minor improvements and bug fixes. Evalute the permutation 3 P 3 A permutation is a way to order or arrange a set or number of things The formula for a combination of choosing r ways from n possibilities is: where n is the number of items and r is the number of arrangements.
Permute gives you choices: you can process each image individually or hit the “Play” button below to convert the images as a big group.
The conversion presets are where Permute really shines. There are numerous popular presets to choose from. If you have a special preset (say, converting images to PNG at 2500px by 2500px), you can make and save your own presets very easily.
I do image and movie file conversions almost every day. For me, Permute 3 is well worth the asking price. It’s a well polished app with a friendly UI that saves me heaps of time. If you’re in the market for the Swiss Army knife tool for file conversions on the Mac, Permute’s the one to get.
-Krishna
Calculator Use
Like the Combinations Calculator the Permutations Calculator finds the number of subsets that can be taken from a larger set. However, the order of the subset matters. The Permutations Calculator finds the number of subsets that can be created including subsets of the same items in different orders.
- Factorial
- There are n! ways of arranging n distinct objects into an ordered sequence, permutations where n = r.
- Combination
- The number of ways to choose a sample of r elements from a set of n distinct objects where order does not matter and replacements are not allowed.
- Permutation
- The number of ways to choose a sample of r elements from a set of n distinct objects where order does matter and replacements are not allowed. When n = r this reduces to n!, a simple factorial of n.
- Combination Replacement
- The number of ways to choose a sample of r elements from a set of n distinct objects where order does not matter and replacements are allowed.
- Permutation Replacement
- The number of ways to choose a sample of r elements from a set of n distinct objects where order does matter and replacements are allowed.
- n
- the set or population
- r
- subset of n or sample set
Permutations Formula:
For n ≥ r ≥ 0.
Calculate the permutations for P(n,r) = n! / (n - r)!. 'The number of ways of obtaining an ordered subset of r elements from a set of n elements.'[1]
Permutation Problem 1
Choose 3 horses from group of 4 horses
In a race of 15 horses you beleive that you know the best 4 horses and that 3 of them will finish in the top spots: win, place and show (1st, 2nd and 3rd). So out of that set of 4 horses you want to pick the subset of 3 winners and the order in which they finish. How many different permutations are there for the top 3 from the 4 best horses?
For this problem we are looking for an ordered subset of 3 horses (r) from the set of 4 best horses (n). We are ignoring the other 11 horses in this race of 15 because they do not apply to our problem. We must calculate P(4,3) in order to find the total number of possible outcomes for the top 3 winners.
P(4,3) = 4! / (4 - 3)! = 24 Possible Race Results
If our 4 top horses have the numbers 1, 2, 3 and 4 our 24 potential permutations for the winning 3 are {1,2,3}, {1,3,2}, {1,2,4}, {1,4,2}, {1,3,4}, {1,4,3}, {2,1,3}, {2,3,1}, {2,1,4}, {2,4,1}, {2,3,4}, {2,4,3}, {3,1,2}, {3,2,1}, {3,1,4}, {3,4,1}, {3,2,4}, {3,4,2}, {4,1,2}, {4,2,1}, {4,1,3}, {4,3,1}, {4,2,3}, {4,3,2}

Permutation Problem 2
Choose 3 contestants from group of 12 contestants
At a high school track meet the 400 meter race has 12 contestants. The top 3 will receive points for their team. How many different permutations are there for the top 3 from the 12 contestants?
For this problem we are looking for an ordered subset 3 contestants (r) from the 12 contestants (n). We must calculate P(12,3) in order to find the total number of possible outcomes for the top 3.
P(12,3) = 12! / (12-3)! = 1,320 Possible Outcomes
Permutation Problem 3

Choose 5 players from a set of 10 players
3 Permute 3
An NFL team has the 6th pick in the draft, meaning there are 5 other teams drafting before them. If the team believes that there are only 10 players that have a chance of being chosen in the top 5, how many different orders could the top 5 be chosen?
10 Permute 3
For this problem we are finding an ordered subset of 5 players (r) from the set of 10 players (n).

10 Permute 3
P(10,5)=10!/(10-5)!= 30,240 Possible Orders
References
Permute 3
[1] For more information on permutations and combinations please see Wolfram MathWorld: Permutation.
