- The Number Of Carbon Atoms Per Unit Cell Of Diamond Unit Cell Is (a). 6 (b). 1 (c). 4 (d). 8
- The Number Of Carbon Atoms Per Unit Cell Of Diamond Unit Cell Is Determined
- The Number Of Carbon Atoms Per Unit Cell Of Diamond Unit Cell Is Equal
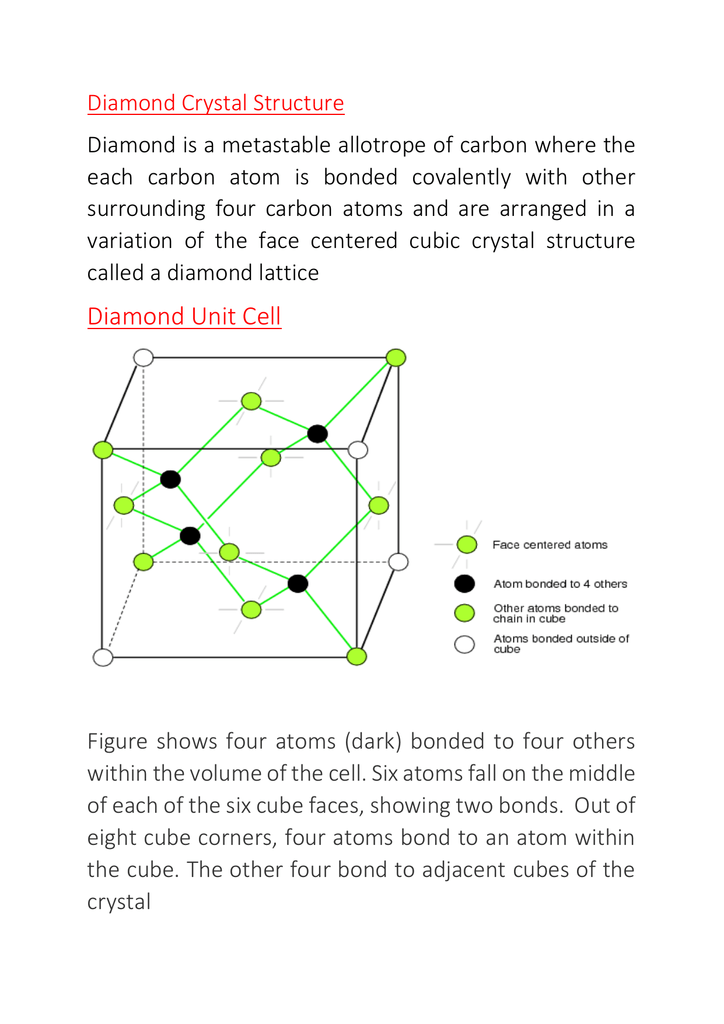
Now, you can see there are 4 carbon atoms inside the unit cell which have full contribution. Therefore we can say that in total = 4 + 1 + 3 = 8 atoms of carbon can be found in making of a unit cell of diamond. The volume of the unit cell then is the edge cubed (edge 3). But the unit cell only contains, on the lattice points, an eighth of the volume of the sphere (ion or atoms). Because there are a total of eight one eighth volume spheres in the cell the simple cubic unit contains one net particle.
| Crystalline Lattices |
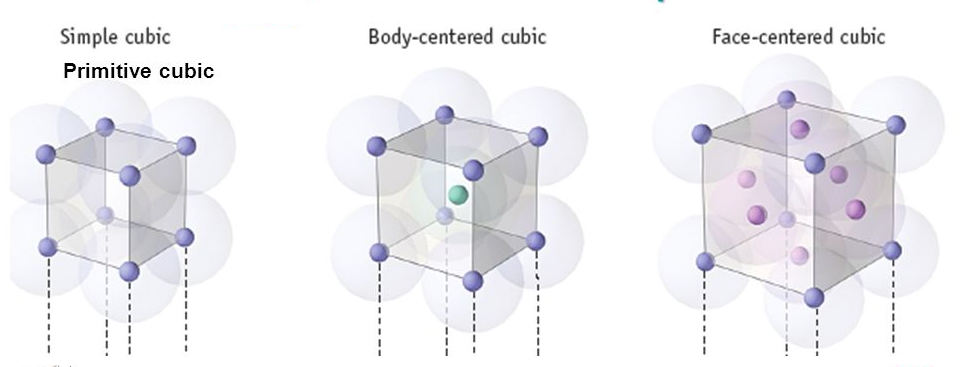
A. Simple Cubic Cell
As you rotate the spacefill model around you will notice that all the spheres (ions or atoms) are in contact with each other. Observe that in the simple cubic cell the edge equals two atomic radii. The volume of the unit cell then is the edge cubed (edge3). But the unit cell only contains, on the lattice points, an eighth of the volume of the sphere (ion or atoms). Because there are a total of eight one eighth volume spheres in the cell the simple cubic unit contains one net particle. One important question should be asked: what is the efficiency of packing same size atoms in simple cubes? |
B. Body-centered Cubic Cell
Rotate the body-centered cubic (bcc) unit cell. As the name suggests it contains an ion or atom in the center of the cube. If all the spheres have the same radius, like in metals, then the spheres centered on the lattice points do not make contact with each other. Another way of looking at the layout is using 2-dimensional layer diagrams. The bcc has 3 layers (along the z-axis), which would look like this: |
So in this case the edge is greater than two atomic radii of the lattice corners. To determine the edge value we must rely on the diagonal of the two opposite corners of the unit cell. This cube diagonal is 4 atom radius. (See calculation).
The number of particles in a bcc unit cell is 2, determined as follows: 8 spheres on the lattice corners each with an eighth of their volume within the cell (1 particle) and one sphere completely embedded in the lattice.
We might expect to have a greater packaging efficiency because there are more particles within the lattice compared to a simple cubic cell. But we should realize that the lattice volume has increased accordingly. The ratio of the volumes where all particles are equal gives us a 68.0%.
Potassium (alkali metal) and iron are examples of metals that arrange themselves in bcc. The virus that causes foot and mouth disease in animals also exhibits bcc crystal arrangements.
C. Face-centered Cubic Cell
Illustrated left is the face-centered cubic (fcc) unit cell. It has a particle in the middle of each of the six faces of the cube. The two-dimensional layer representation shows that there are six particles which have half of their volumes within the lattice. The total number of particles within the lattice can be calculated as follows: 8 particles on the lattice corners (1 particle), 6 particles with half of their volumes within the lattice (6 particles* 1/2 volume = 3 particles). This gives us a total of 4. Calculation of the edge value is quite straightforward. (See figure for calculations) |
Face-centered cubic cells have a 74.0% packaging efficiency for spheres or ions of equal diameter. Some examples of fcc arrangements are: aluminum, copper and buckminsterfullerenes C60 (bucky balls).
It is crucial that we consider that there are holes within these lattices (rotate the 3D fcc model) which can be filled with smaller ions or particles - we will see this later - thus increasing packaging efficiency. Compounds like salts fulfill this requirement. Ions of opposite charge can occupy these spaces. The result is an organized three-dimensional arrangement of ions and counter-ions.
D. Ionic Compounds
Ionic compounds are made up of anions and cations. Usually the larger anions make up the framework of the crystal lattice and the smaller cations then occupy the spaces or holes left between the framework of anions. Packing arrangements like simple cubic (sc), cubic close-packed (ccp), hexagonal close-packed (hcp) are examples of structures which minimize same charge interactions.
Let's start with anions packing in simple cubic cells. Avast small office protection. As you can see in Figure 6 the cation can sit in the hole where 8 anions pack. An example of this packing is CsCl (See the CsCl file left; Cl- yellow, Cs+ green). This lattice framework is arrange by the chloride ions forming a cubic structure. The smaller cesium cation sits in the hole surrounded by 8 chloride ions. Alternatively, it can be viewed as a chloride anion surrounded by 8 cesium cations. Both have coordination number 8. Each unit cell has one cesium ion and one chloride ion. The cubic hole is quite large. Compare the sizes of Cs+ (1.69 Å) to Cl- (1.81 Å). It is convenient at this point to clarify the misconception concerning CsCl arrangement. Cesium chloride does not pack in a body-centered cubic structure. In a body-centered cubic structure all the atoms in the unit cell are identical (See section on Body- centered Cubic Cell). As you may have noticed the cation occupying the center of the cube is smaller than the anions on the corners of the cube. |
The Octahedral Hole
The octahedron is a polyhedron made from 8 regular triangles. The polyhedron can be constructed by one sphere surrounded by 6 equal spheres (Figure 7A). If you connect the six centers of the surrounding spheres you generate the octahedron.
Face-centered cubic (fcc) lattice structures provide a framework for octahedral holes. A typical example of this setting is sodium chloride (NaCl). The chloride ions form octahedral holes which the smaller sodium ions occupy. (See 3D NaCl file right; Na+ fuchsia, Cl- green) There are 4 octahedral holes in a fcc with a relationship of one octahedral hole per anion.
It is important to notice that Na+ ions can be viewed as an expanded fcc where the chloride ions occupy large octahedral holes. This arrangement of ions give the Na+ ion as well as the Cl- ion a coordination number of 6. Each unit cell thus contains 4 Na+ and 4 Cl-, with stoichiometry NaCl (Figure 7B).
There are compounds where not all the octahedral holes are filled. In the case of cadmium chloride, CdCl2 (Figure 8), the large chloride ions form a fcc framework. Only half of the octahedral holes are filled by the smaller cadmium ions, therefore, there will be 2 cadmium ions in a unit cell. At the same time the fcc unit cell framework of the large anions contains 4 Cl- ions. Consequently, the stoichiometry for cadmium chloride is CdCl2.
The Number Of Carbon Atoms Per Unit Cell Of Diamond Unit Cell Is (a). 6 (b). 1 (c). 4 (d). 8
The Tetrahedral Hole
A classic example used to view a tetrahedral structure is methane, CH4. The carbon atom has four equally distanced hydrogen atoms, each positioned on the corners of a tetrahedron. The same idea can be applied to close-pack spheres (Figure 9A). A sphere occupying a tetrahedral hole has a coordination number of 4. Tetrahedral holes are relatively small compared to cubic or octahedral holes.
A fcc arrangement has both tetrahedral and octahedral holes. (Move your mouse over Figure 9B and see also the location of the octahedral holes in a cubic close-pack structure.) There are 8 tetrahedral holes and 4 octahedral holes in a fcc unit cell.
The ionic compound sodium oxide is a good example of a fcc cell where the oxide ions form the framework of the unit cell while the quite small sodium ions occupy all the tetrahedral holes. As we take a closer look at the lattice (see the sodium oxide 3D file right; O2- red and Na+ pink, and Figure 10A) you will notice that there are 4 oxide ions (eight of them at the corners of the cube with 1/8 of their volume inside the cell and 6 centered on each face sharing half of their volume with the unit cell; Figure 10B) and eight sodium ions (occupying all the tetrahedral holes within the unit cell). It follows that there are 2 tetrahedral and 1 octahedral holes per anion in a fcc structure where the anions make the close-pack framework. Thus the coordination number for Na+ is 4 and for O2- is 8. Consequently the stoichiometry for sodium oxide is Na2O.
The Number Of Carbon Atoms Per Unit Cell Of Diamond Unit Cell Is Determined
As expected there can be partial filling of the tetrahedral holes. This is appropriately illustrated by zinc sulfide (sphalerite). The 3D RasMol file for zinc blende is shown left, S2- ions in yellow and Zn2+ in burgundy. The large sulfide ions form the fcc framework. Only half of the tetrahedral holes are filled by the small zinc ions. In order for each ion to have an tetrahedral arrangement the zinc ions should occupy the positions in the lattice such that the line that connects the ionic centers is a diagonal of the cube in each layer and these lines are orthogonal to each other (rotate the 3D zinc blende file to verify this characteristic). Such an arrangement allows each atom to have a coordination number of 4 for which a tetrahedral geometry is viable. Other ionic compounds which exhibit the same zinc blende arrangement are: AgI and CuCl.
It would be appropriate at this point to have a very brief overview of more complex ionic structures. As we saw previously in a cubic close-packed arrangement there are both tetrahedral and octahedral holes. Certain ionic compounds have the structure of the mineral spinel, MgAl2O4. It crystallizes in what is an approximate cubic close-packed structure. The cations, Mg2+ and Al3+, in this structure occupy the tetrahedral and octahedral holes (recall one octahedral hole and 2 tetrahedral holes per anion in an fcc). The unit cell contains 32 oxide ions. That translates into 32 octahedral holes and 64 tetrahedral holes. To have a stoichiometry of 1:2:4 (Mg:Al:O) means that Al3+ ions will occupy half of the available octahedral holes while the Mg2+ ions should fill only an eighth of the available tetrahedral holes. Use the 2D layer diagram below to verify location of each type of hole as well as the stoichiometry of spinel.
The RasMol 3D representation of spinel also helps visualize its unit cell. The light pink atoms represent the anions, O2-, the rose colored atoms represent the Al3+ in the octahedral holes and finally the white atoms represent the Mg2+ ions in the tetrahedral holes.
Magnetite, Fe3O4, has the same approximate fcc arrangement with the oxide anions occupying the lattice framework but the octahedral holes are occupied by both divalent and trivalent iron cations. As a result octahedral holes in the magnetite spinel arrangement are filled with equal amounts of Fe3+ and Fe2+ ions. Charge balance and the general arrangement of cations and anions is preserved.
The Number Of Carbon Atoms Per Unit Cell Of Diamond Unit Cell Is Equal
There are also molecular networks which can be seen as exhibiting an expanded fcc framework with partial filling of the tetrahedral holes. As as example we have diamond. We can think of it as carbon atoms forming the expanded fcc framework and also occupying half the tetrahedral holes. This arrangement is also common to semiconductors like SiC (silicon carbide) and BN (boron nitride) and GaAs (gallium arsenide) among others. We have to keep in mind that in molecular networks (such as diamond) the coordination number is the number of bonds around each atom. Observe on the left the 3D silicon carbide file (carbon atoms in gray, silicon atoms in yellow) and Figure 11 on the right.
References
Ellis, A.B., Geselbracht, M.J., Johnson, B.J., Lisensky, G.C., Robinson, W.R. Teaching General Chemistry: A Material Science Companion, American Chemical Society, Washington, DC, 1993.
Lambert, J. Spinel Models for Demonstrating Crystal Field Stabilization, Journal of Chemical Education, 41 (1); 41-3, Jan. 1964
Webmaster
José Laboy, University of Wisconsin-Madison, August 2010.
